卡尔曼滤波以及代码分析 #
什么是卡尔曼滤波 #
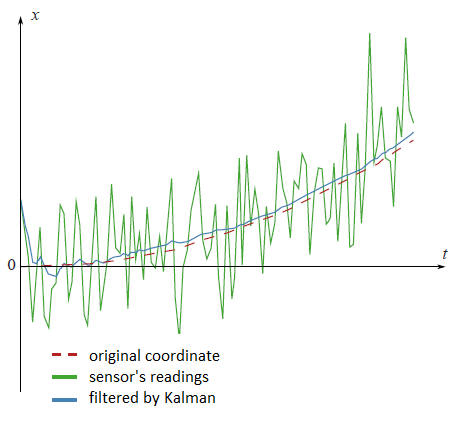
根据维基百科的描述:卡尔曼滤波(Kalman filter)是一种高效率的递归滤波器(自回归滤波器),它能够从一系列的不完全及包含噪声的测量中,估计动态系统的状态。下面一张图展示了滤波前与滤波后的区别:传感器直接获取的数据是绿色线,真实坐标是红色虚线,而经过卡尔曼滤波之后的数据是蓝线。可见,卡尔曼滤波极大的提高了数据的稳定性,降低了噪声对其的影响。
卡尔曼滤波的原理 #
卡尔曼滤波的原理并不复杂,理解它只要拥有矩阵运算与概率论的基础就足够了。
状态的表示 #
假设我们需要预测一个机器人的运动,很明显,我们可以想到与运动相关的两个数据是速度与位置。在这里,我们采用 \(\mathbf{x}\) 来表示机器人的状态, \(\mathbf{p}\) 来代表机器人的位置 (Position), \(\mathbf{v}\) 来代表机器人的速度 (Velocity)。那么我们有如下的式子: \[\mathbf{x} = \begin{bmatrix} \mathbf{p} \\ \mathbf{v} \end{bmatrix} ~~~~ \mathbf{p} = \begin{bmatrix} p_x \\ p_y \\ p_z \end{bmatrix} ~~~~ \mathbf{v} = \begin{bmatrix} v_x \\ v_y \\ v_z \end{bmatrix}\]
我们并不知道 \(\mathbf{x}\) 的实际值,卡尔曼滤波假设, \(\mathbf{x}\) 符合二维正态分布,也就是下面这张图:
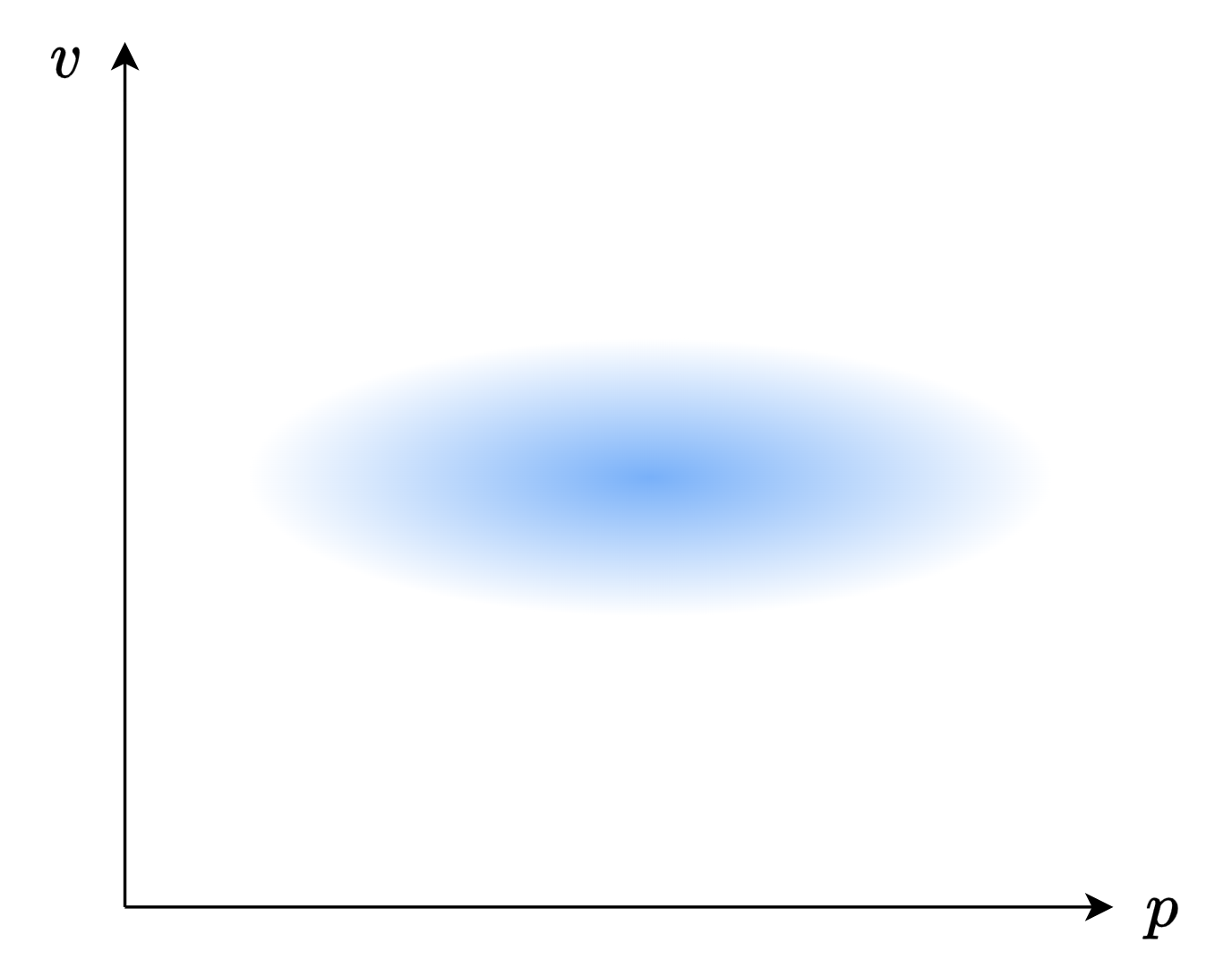
图中,蓝色的深浅表示概率的高低。当然,如果你学过概率论,你可以看出来,这个图里面的位置 \(\mathbf{p}\) 与速度 \(\mathbf{v}\) 是独立的。而实际上,它们之间应当是有一定的关系的,因为机器人的速度越快,它的位置可能就越远!就像下面这张图一样:
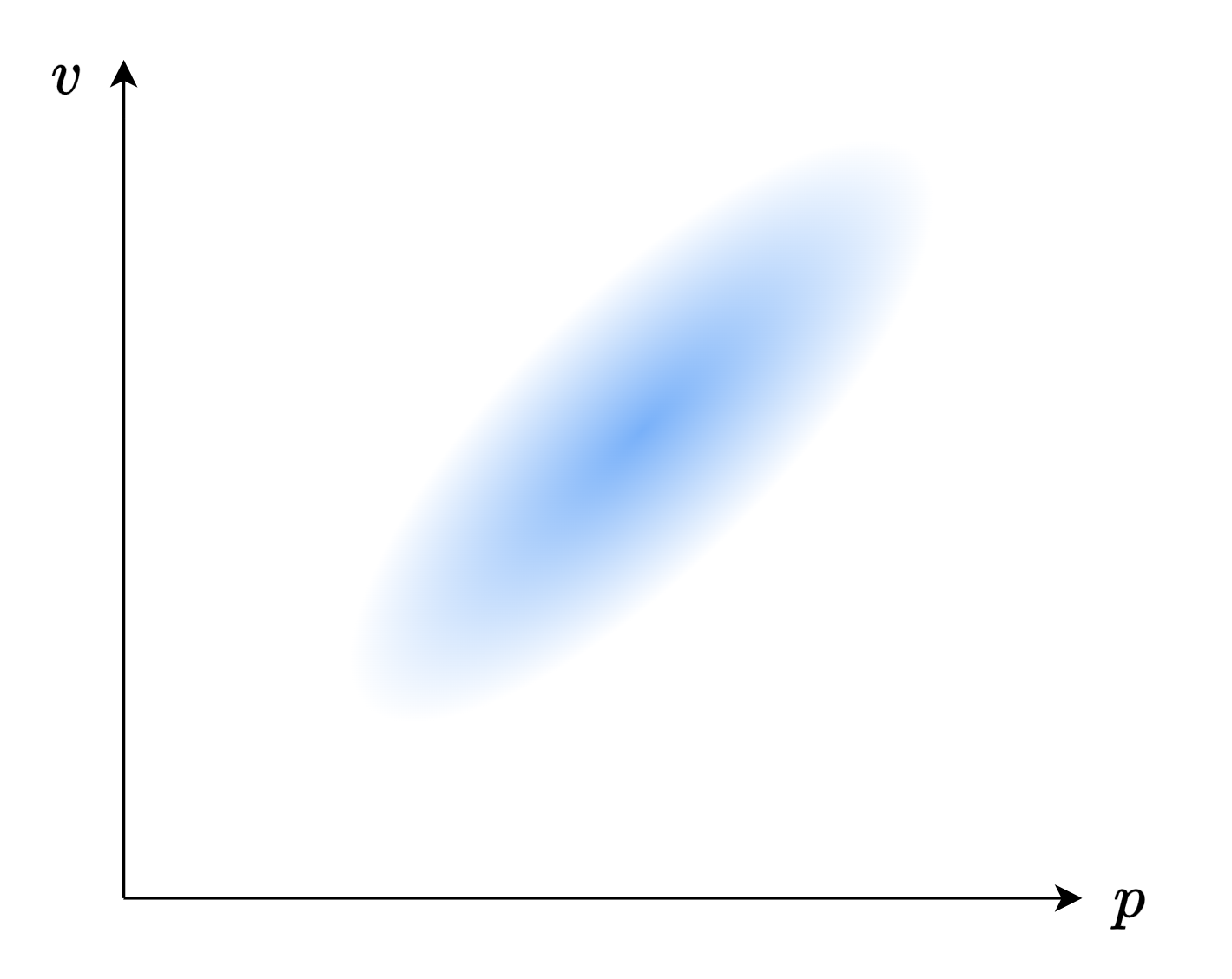
为了捕获这种相关性的信息,我们就要用到协方差矩阵。在这里,我们采用 \(\Sigma_{AB}\) 来表示 \(A\) 与 \(B\) 的协方差矩阵。我们就可以得到如下的描述: \[\mathbf{x} = \begin{bmatrix} \mathbf{p} \\ \mathbf{v} \end{bmatrix} ~~~~ \mathbf{P} = \begin{bmatrix} \Sigma_{pp} & \Sigma_{pv} \\ \Sigma_{vp} & \Sigma_{vv} \end{bmatrix}\]
这里的 \(\mathbf{x}\) 就是所谓的系统状态矩阵, \(\mathbf{P}\) 就是所谓的状态估计协方差。
预测过程 #
现在,假设我们已经知道了某一时刻 \(k\) 的 \(\mathbf{x}\) 与 \(\mathbf{P}\) 。为了方便表示,我们将 \(k\) 时刻的 \(\mathbf{x}\) 写作 \(\mathbf{x}_k\) , \(\mathbf{P}_k\) 也是同理。而这个递推过程称为预测。
那么,我们需要做的工作就是预测下一时刻的 \(\mathbf{x}\) 与 \(\mathbf{P}\) ,也就是 \(\mathbf{x}_{k+1}\) 与 \(\mathbf{P}_{k+1}\)
看下面这张图,假设蓝色代表了 \(\mathbf{x}_k\) 的分布,而绿色代表了 \(\mathbf{x}_{k+1}\) 的分布。根据矩阵相乘的知识,我们可以使用矩阵 \(\mathbf{A}\) 来代表这个预测过程。也就是 \[\mathbf{Ax}_{k}=\mathbf{x}_{k+1}\]
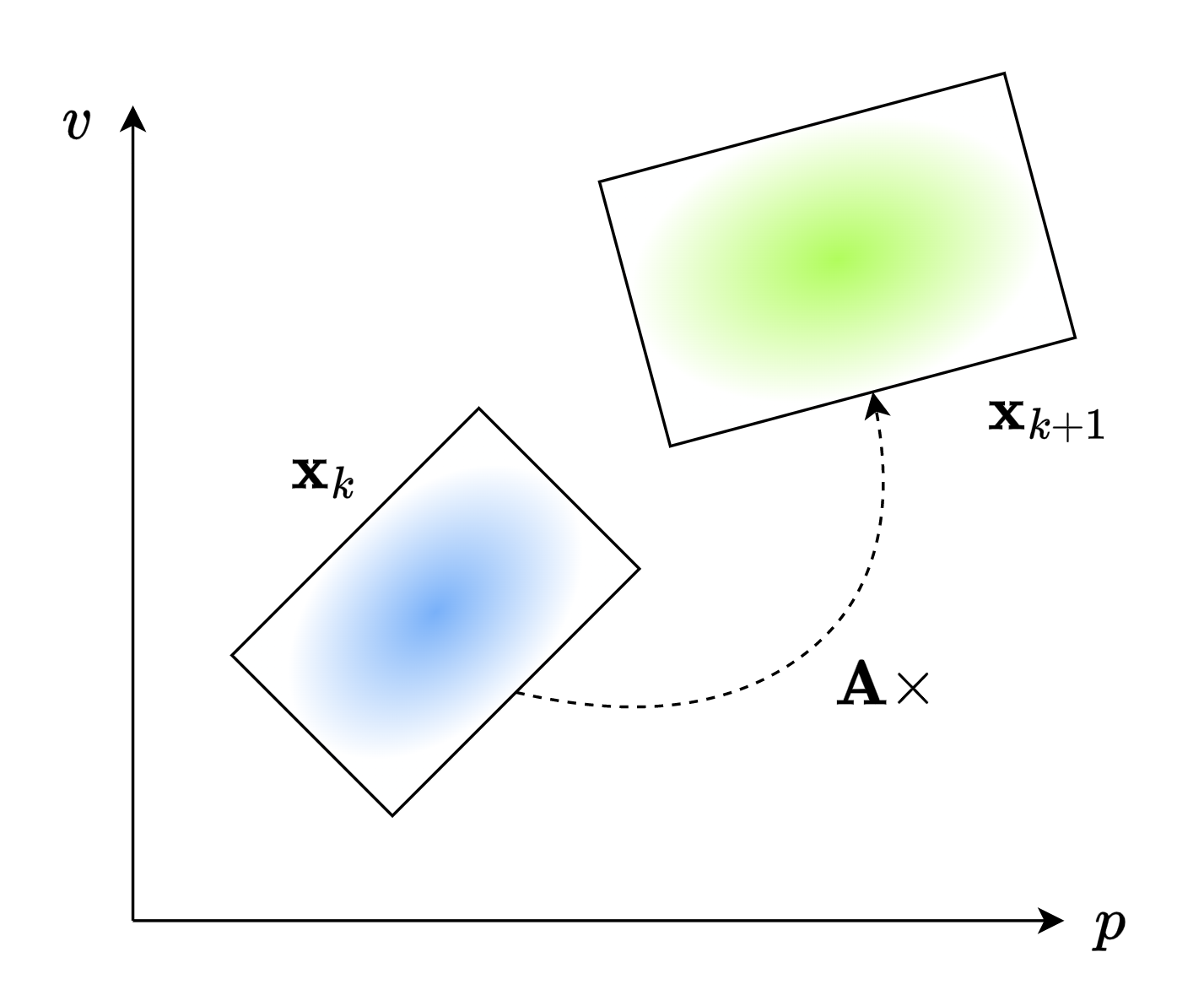
\(\mathbf{A}\) 就是所谓的状态转移矩阵。 那这个 \(\mathbf{A}\) 应当怎么获取呢?
我们假设机器人的运动是匀速的,根据高中物理的知识,一维匀速运动的物体的位置 \(p\) 与速度 \(v\) 满足下面的关系: \[\begin{aligned} p &= p_0 + v_0 \Delta t \\ v &= v_0 \end{aligned}\]
三维的匀速运动就是一维的匀速运动的叠加,反映到矩阵上,也就是 \[\begin{aligned} \mathbf{x}_{k+1} &= \begin{bmatrix} \mathbf{p}_k + \mathbf{v}_k \Delta t \\ \mathbf{v}_k \end{bmatrix} \\ &=\begin{bmatrix} 1 & \Delta t \\ 0 & 1 \end{bmatrix} \begin{bmatrix} \mathbf{p}_k \\ \mathbf{v}_k \end{bmatrix} \\ &= \mathbf{Ax}_k \end{aligned}\]
这里的 \(\mathbf{A}\) 为了方便表示,采用了 \(2\times 2\) 矩阵,但实际上,它的大小取决于 \(\mathbf{x}\) 的大小,例如,在三维中, \(\mathbf{x}\) 是 \(6\times 1\) 的向量,所以 \(\mathbf{A}\) 应该是 \(6\times 6\) 的大小。展开来写,也就是:
\[\begin{aligned} \mathbf{x}_{k+1} &=\begin{bmatrix} 1 & 0 & 0 & \Delta t & 0 & 0 \\ 0 & 1 & 0 & 0 & \Delta t & 0 \\ 0 & 0 & 1 & 0 & 0 & \Delta t \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} p_x \\ p_y \\ p_z \\ v_x \\ v_y \\ v_z \\ \end{bmatrix} \end{aligned}\]如果你去看代码,这个 \(6\times 6\) 的矩阵就是 \(\mathbf{A}\) ,也就是所谓的状态转移矩阵。
我们知道了如何更新 \(\mathbf{x}\) ,接下来我们就需要知道如何更新 \(\mathbf{P}\) 。好在,在概率论中,我们有公式可以直接套用: \[\begin{aligned} Cov(x) &= \Sigma \\ Cov(\mathbf{A}x) &= \mathbf{A} \Sigma \mathbf{A}^\top \end{aligned}\]
根据这个公式,我们有: \[\mathbf{P}_{k+1} = \mathbf{A} \mathbf{P}_k \mathbf{A}^\top \]
所以,我们就得到了如何通过 \(\mathbf{x}_k\) 与 \(\mathbf{P}_k\) 来求得 \(\mathbf{x}_{k+1}\) 与 \(\mathbf{P}_{k+1}\) :
\[\begin{aligned} \mathbf{x}_{k+1} &= \mathbf{Ax}_k \\ \mathbf{P}_{k+1} &= \mathbf{A} \mathbf{P}_k \mathrm{A}^\top \end{aligned}\]在我们的预测中,同样也应该考虑噪声的影响。这可能是各种其他奇奇怪怪的因素造成的:无人机可能会被风吹来吹去,车子的轮胎可能会与地面打滑漂移……
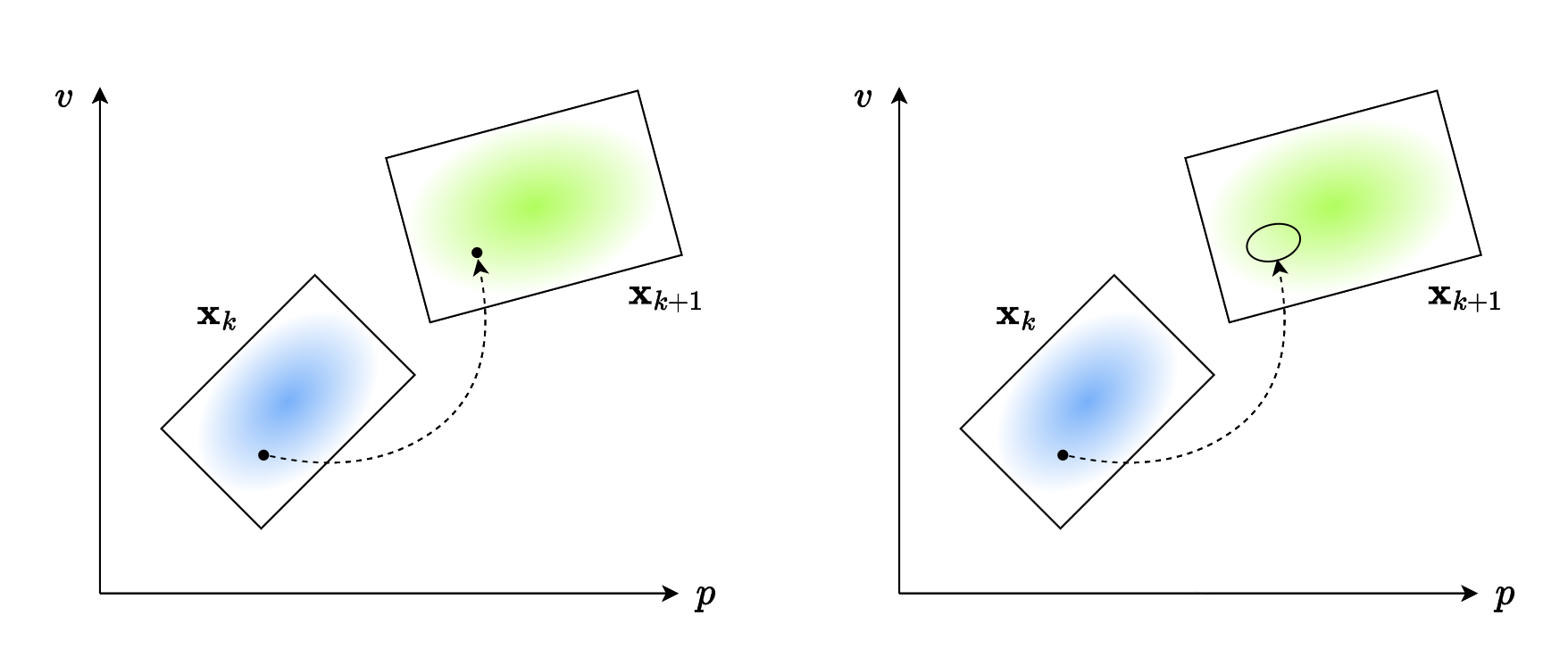
在上一小节中,我们认为状态是“点对点”的,也就是像下图左侧描述的一样。但是,如果我们考虑噪声的影响,状态就不是“点对点”的,而是“点对多”的分布。 就像下图右侧所表示的一样。
这并不会干扰 \(\mathbf{x}_{k+1}\) 的均值,但是会确确实实影响 \(\mathbf{x}_{k+1}\) 的方差。就像下图所示:虚线是原来的分布,而实线是考虑噪声后的分布。它的中心没有改变,但方差却变大了。
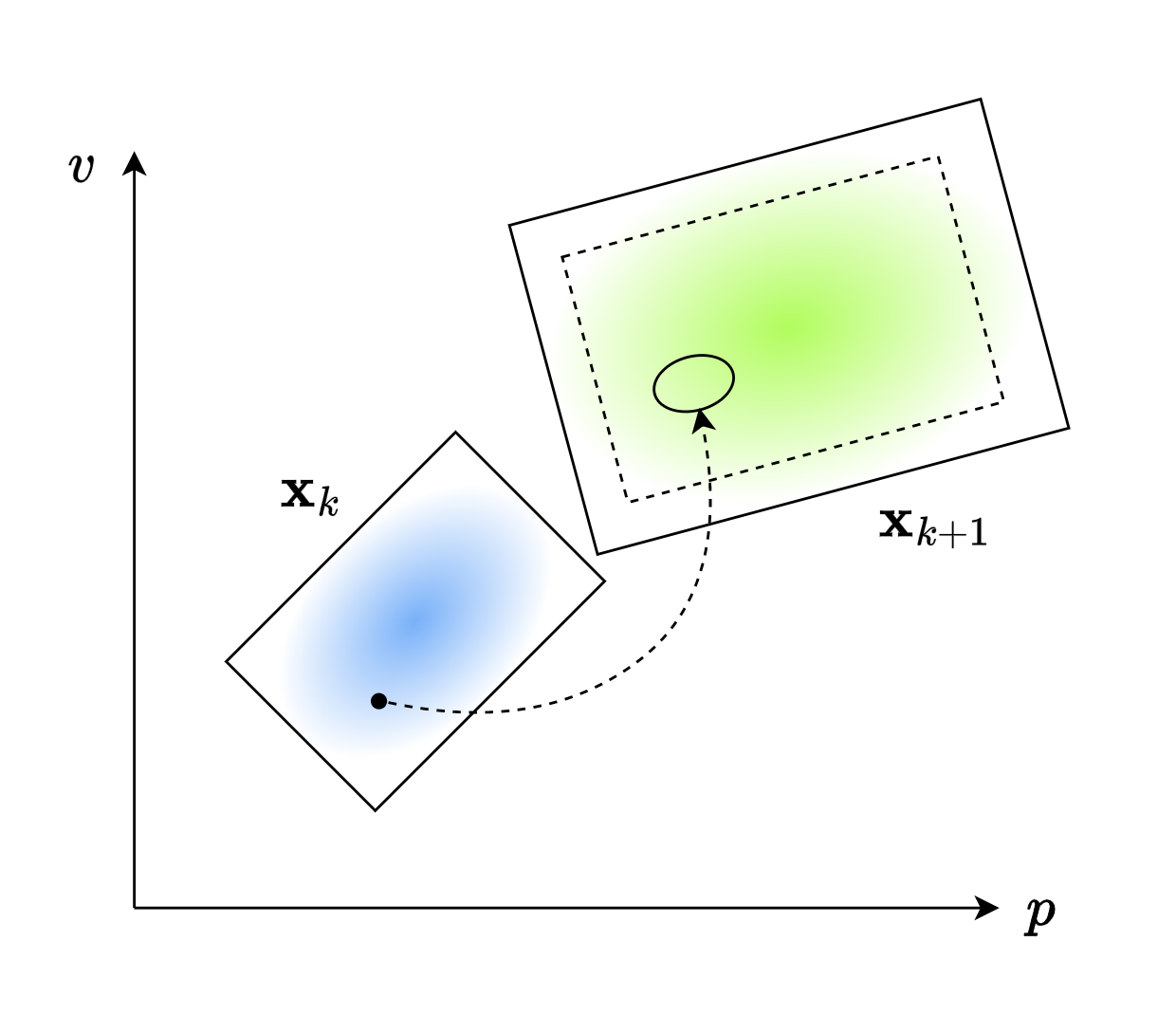
为了描述这一变化,我们使用 \(\mathbf{Q}_{k}\) 代表当前时刻外部不确定性,也就是噪声带来的影响。因此我们得到下面的式子:
\[\begin{aligned} \mathbf{x}_{k+1} &= \mathbf{Ax}_k \\ \mathbf{P}_{k+1} &= \mathbf{A} \mathbf{P}_k \mathbf{A}^\top + \mathbf{Q}_{k} \end{aligned}\]更新过程 #
当然,只递推是不行的,我们还要考虑传感器测出来的实际值,并将传感器测出的数据与上一步预测得到的数据进行综合。这个过程称为更新。
假设我们预测 \(k\) 时刻的值,我们计算出了预测值 \(\mathbf{x}_{k}\) ,但是,这与观测值不能直接综合,因为传感器自身有偏差,因此,我们需要加上一个状态观测矩阵 \(\mathbf{H}_{k}\) ,从而计算出我们预测的传感器的测量值。就像下图一样:
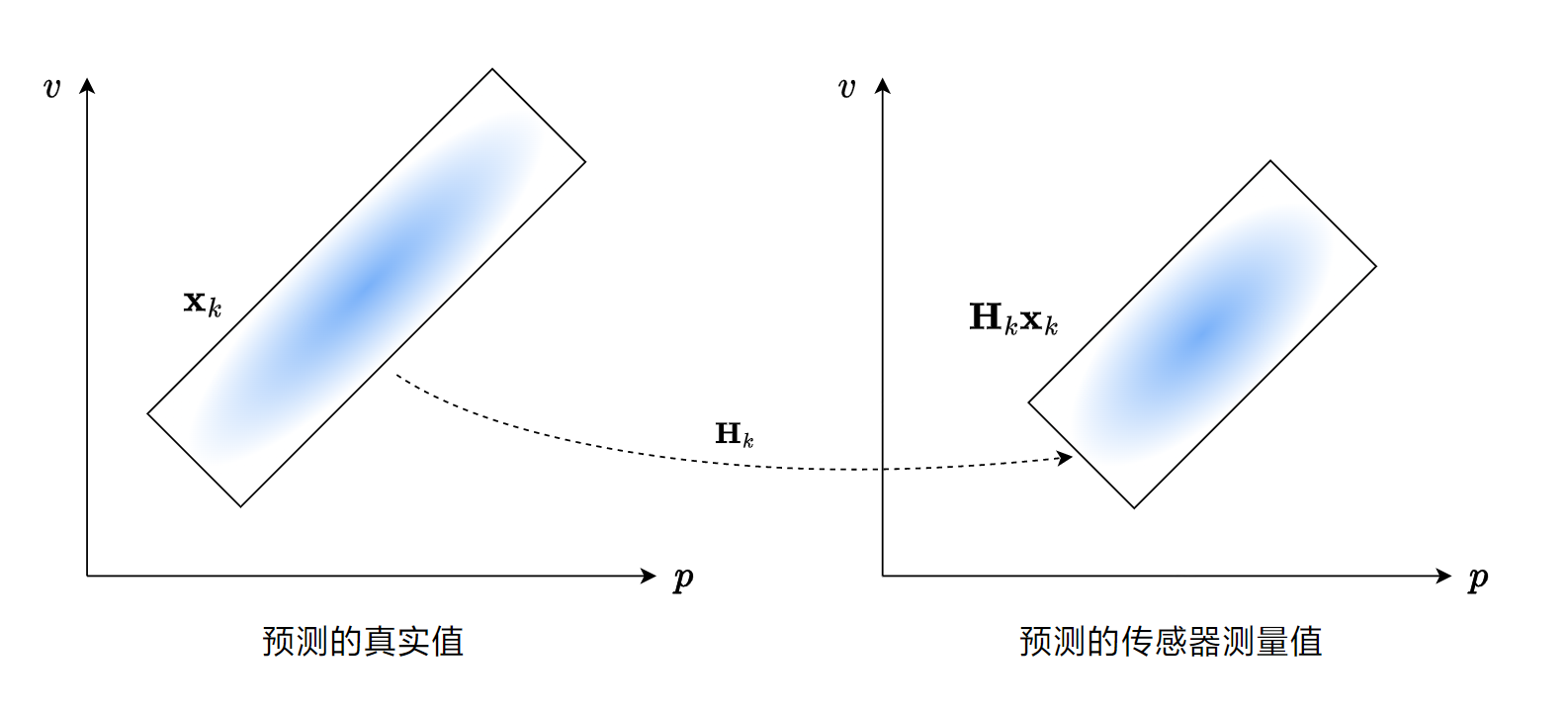
之后,再将这个与传感器测出的数据进行综合,如下图:
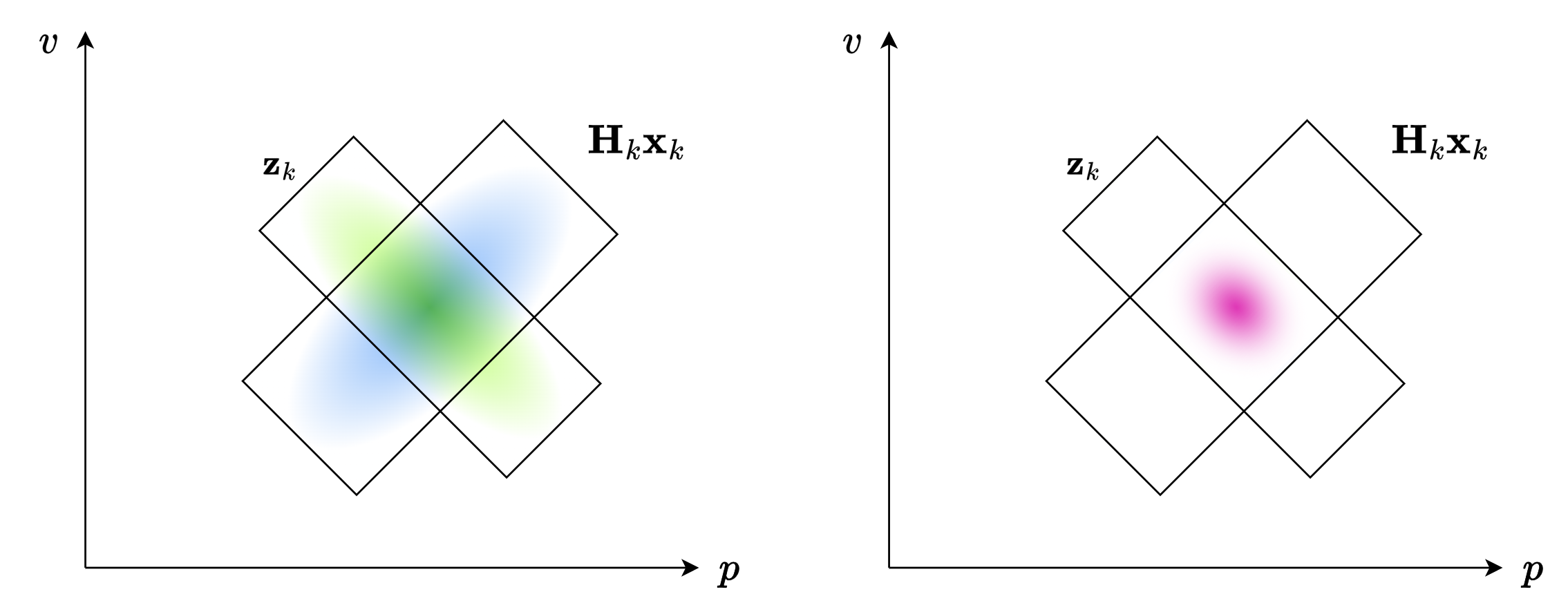
其中,传感器测得的数据为 \(\mathbf{z}_{k}\) ,其协方差矩阵为 \(\mathbf{R}\) 。
传感器测得的数据与预测的数据都是二维正态分布,直接理解这个过程未免有一些困难。在阐述如何将传感器测得的数据与预测的数据进行综合之前,我们不妨先从一个简单的例子开始:如何综合两个一维正态分布?
如下图,假设我们拥有两个正态分布,分别是 \(X_1\) 与 \(X_2\) ,我们需要综合得出 \(X_3\)
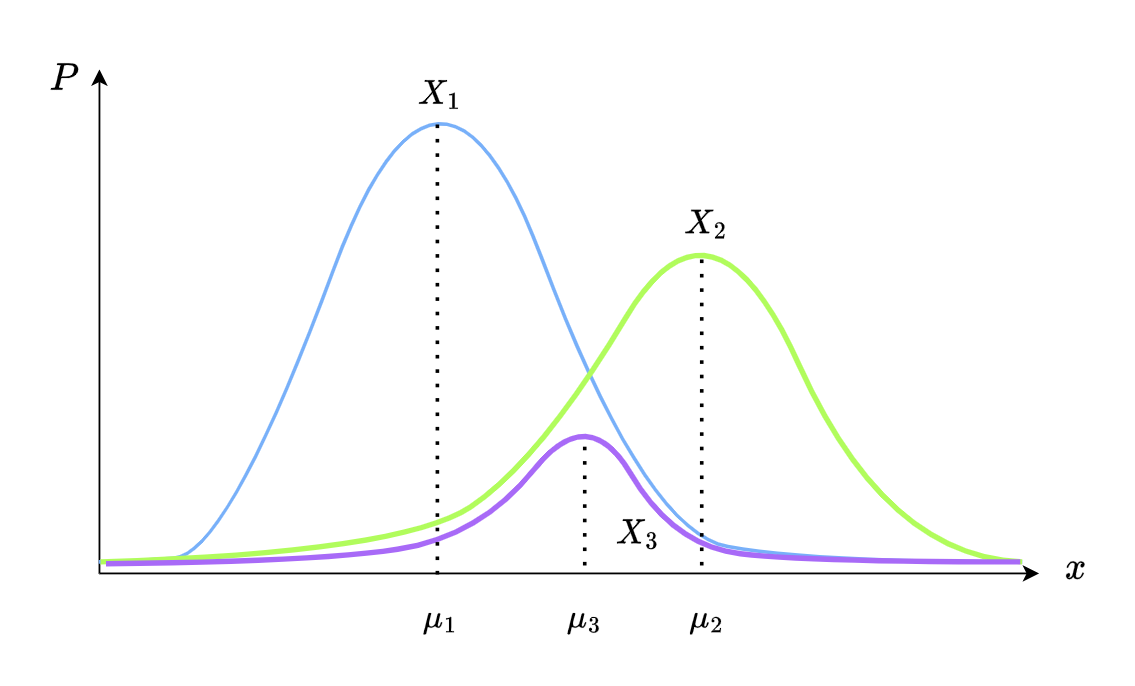
正态分布的公式如下:
\[P(X = x) = \frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{(x - \mu)^2}{2\sigma^2}}\]我们应当怎么综合呢?一个能想到的显而易见的方法就是相乘.在相乘之后,我们可以得到新的正态分布 \(X_3\) 的 \(\mu_3\) 以及 \(\sigma^2_3\)
\[\begin{aligned} \mu_3 &= \frac{\mu_1\sigma^2_2 + \mu_2\sigma^2_1}{\sigma^2_1+\sigma^2_2} \\ \sigma^2_3 &= \frac{\sigma^2_1 \sigma^2_2}{\sigma^2_1+\sigma^2_2} \\ \end{aligned}\]我们不妨假设一个变量 \(K\) 来简化一下这个式子:
\[\begin{aligned} K &= \frac{\sigma^2_1}{\sigma^2_1+\sigma^2_2} \\ \mu_3 &= \mu_1 + K(\mu_2 - \mu_1) \\ \sigma^2_3 &= \sigma_1^2 - K\sigma_1^2 \end{aligned}\]其中,我们把 \(\mu_2 - \mu_1\) 称作 \(\mu\) 的残差。而 \(K\in [~0,1~]\) 则是一个系数, \(K\) 越大,则最后 \(X_3\) 越偏向于 \(X_2\) ,反之,则偏向于 \(X_1\) .
我们将其转成矩阵的格式:
\[\begin{aligned} \mathbf{K} &= \Sigma_0 (\Sigma_0+\Sigma_1)^{-1} \\ \vec{\mu_3} &= \vec{\mu_1} + \mathbf{K}(\vec{\mu_2} - \vec{\mu_1}) \\ \Sigma_3 &= \Sigma_1 - \mathbf{K}\Sigma_1 \end{aligned}\]这个 \(\mathbf{K}\) 就是所谓的 卡尔曼增益。
现在,回到之前的任务,我们有两个正态分布需要综合。

让我们把这两个正态分布写出来:
\[\begin{aligned} (\mu_1, \Sigma_1) &= (\mathbf{H}_k \mathbf{x}_k, \mathbf{H}_k\mathbf{P}_k\mathbf{H}_k^\top) \\ (\mu_2, \Sigma_2) &= (\mathbf{z}_k, \mathbf{R}_k) \end{aligned}\]之后将这两个正态分布代入我们刚才得到的矩阵形式的式子中:
\[\begin{aligned} \mathbf{K} &= \mathbf{H}_k\mathbf{P}_k\mathbf{H}_k^\top (\mathbf{H}_k\mathbf{P}_k\mathbf{H}_k^\top + \mathbf{R})^{-1} \\ \mathbf{H}_k \hat{\mathbf{x}_k} &= \mathbf{H}_k \mathbf{x}_k + \mathbf{K} (\mathbf{z}_k - \mathbf{H}_k \mathbf{x}_k) \\ \mathbf{H}_k\hat{\mathbf{P}_k}\mathbf{H}_k^\top &= \mathbf{H}_k\mathbf{P}_k\mathbf{H}_k^\top - \mathbf{K} \mathbf{H}_k\mathbf{P}_k\mathbf{H}_k^\top \end{aligned}\]其中, \(\hat{\mathbf{x}_k}\) 与 \(\hat{\mathbf{P}_k}\) 代表我们综合之后的估计值。
我们给 \(\mathbf{K}\) 去掉一个 \(\mathbf{H}_k\) ,再去掉等号左边多余的 \(\mathbf{H}_k\) 与 \(\mathbf{H}_k\) 与 \(\mathbf{H}_k^\top\) ,得到:
\[\begin{aligned} \mathbf{K} &= \mathbf{P}_k\mathbf{H}_k^\top (\mathbf{H}_k\mathbf{P}_k\mathbf{H}_k^\top + \mathbf{R})^{-1} \\ \hat{\mathbf{x}_k} &= \mathbf{x}_k + \mathbf{K} (\mathbf{z}_k - \mathbf{H}_k \mathbf{x}_k) \\ \hat{\mathbf{P}_k} &=( \mathbf{I} - \mathbf{K} \mathbf{H}_k)\mathbf{P}_k \end{aligned}\]这就是卡尔曼滤波的更新公式了。
再加上之前的预测公式,就是卡尔曼滤波的所谓黄金五条:
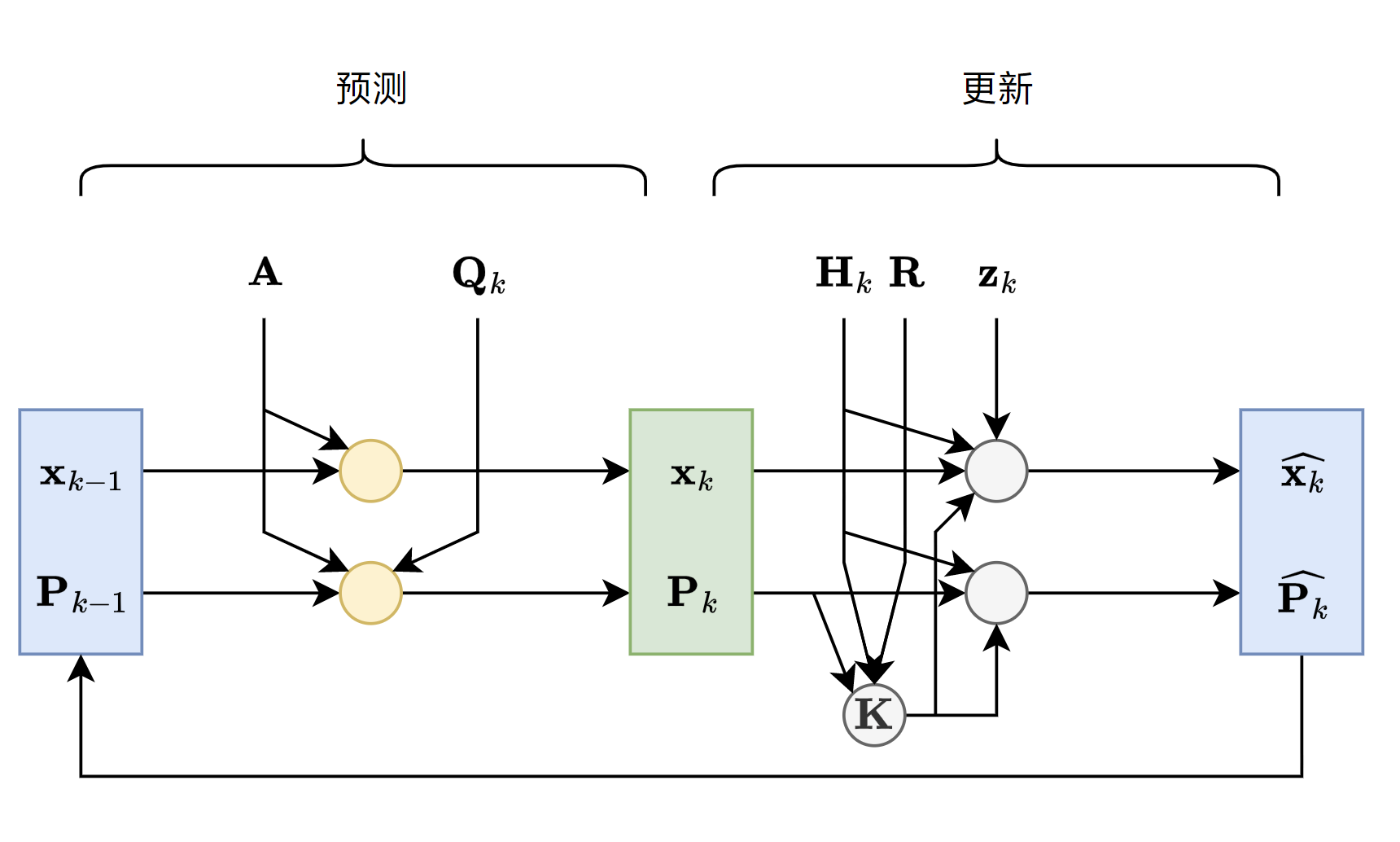
\[\begin{aligned} \mathbf{x}_{k} &= \mathbf{Ax}_{k-1} \\ \mathbf{P}_{k} &= \mathbf{A} \mathbf{P}_{k+1} \mathbf{A}^\top + \mathbf{Q}_{k-1}\\ \mathbf{K} &= \mathbf{P}_k\mathbf{H}_k^\top (\mathbf{H}_k\mathbf{P}_k\mathbf{H}_k^\top + \mathbf{R})^{-1} \\ \hat{\mathbf{x}_k} &= \mathbf{x}_k + \mathbf{K} (\mathbf{z}_k - \mathbf{H}_k \mathbf{x}_k) \\ \hat{\mathbf{P}_k} &=( \mathbf{I} - \mathbf{K} \mathbf{H}_k)\mathbf{P}_k \\ \end{aligned}\]最后,放一张总的流程图,图中的每一个圆圈都代表黄金五条中的一个式子。