从 AE 到 VAE 再到 VQ-VAE #
自编码器 (AE) #
让我们从最早的自编码器 (Auto Encoder, AE) 开始一步一步谈起. AE 是一类能够把图片压缩成较短的向量的神经网络模型. 包含两部分:
- 编码器 $e$: 负责将输入 $\mathbf x$ 映射为一个较短的向量 $\mathbf z$. 也就是 $e(\mathbf x)=\mathbf z$
- 解码器 $d$: 负责从 $\mathbf z$ 重建为与 $\mathbf x$ 接近的 $\hat\mathbf x$. 也就是 $d(\mathbf z) =\hat\mathbf x$
自编码器的训练目标是最小化 $\mathbf x$ 与 $\hat\mathbf x$ 的区别. 例如,使用均方差损失 $$\mathcal L = \frac{1}{N}\sum_i (x_i - \hat x_i)^2$$
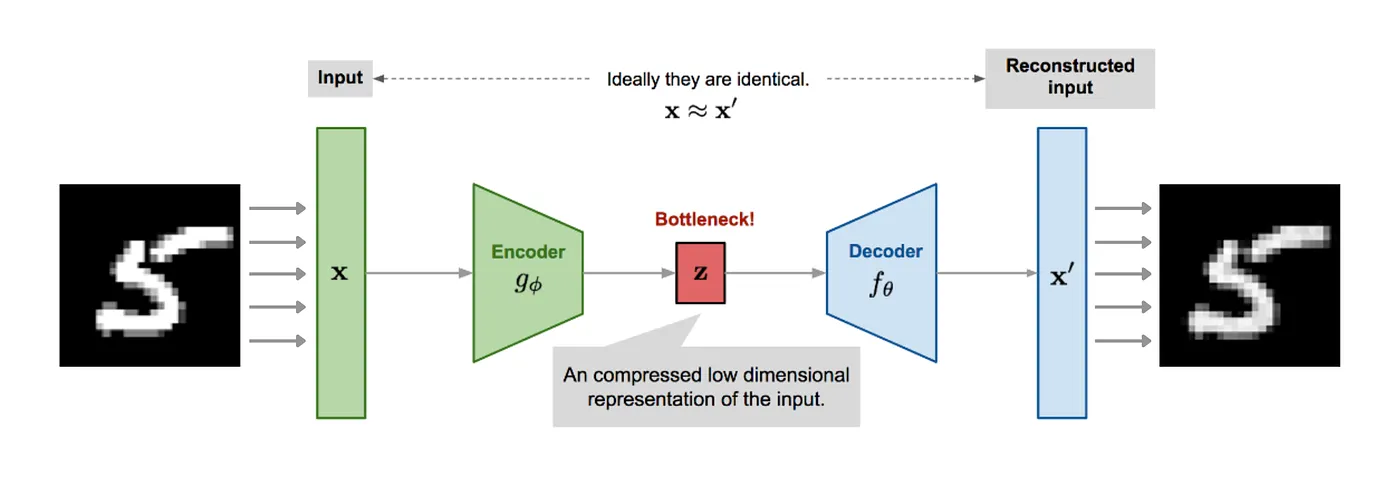
一个简单的想法是训练完编码器与解码器之后将编码器丢掉, 只留下解码器. 这样我们随机生成一个 $\mathbf z$ 就可以生成一个 $\hat\mathbf x$. 但这样实际上是不行的. 一个简单的例子如下:

之所以会导致这种问题, 是因为 $\mathbf z$ 服从一个我们未知的分布. 解码器只能从这个分布中采样的 $\mathbf z$ 重建有意义的图像. 对于不是从这个分布中采样的 $\mathbf z$, 解码器大概率会输出无意义的图像.
变分自编码器 (VAE) #
自编码器距离做图像生成任务就差一步了. 只要我们能把 $\mathbf z$ 约束到一个我们能采样的分布上, 我们就可以用解码器来做图像生成. 这就是 VAE 的思路.
VAE 的核心改进就是将编码器的输出从一个向量 $\mathbf z$ 换成这个向量 $\mathbf z$ 的分布. 我们假设 $P(\mathbf z|\mathbf x)$ 服从正态分布. 那么编码器的输出就是这个正态分布的均值 $\boldsymbol{\mu}_{\mathbf z | \mathbf x}$ 与方差 $\boldsymbol{\sigma}^2_{\mathbf z | \mathbf x}$. 而真正的 $\mathbf z$ 从这个分布进行采样. 这样就可以通过将 $\boldsymbol{\mu}_{\mathbf z | \mathbf x}$ 与方差 $\boldsymbol{\sigma}^2_{\mathbf z | \mathbf x}$ 添加到优化目标来对 $\mathbf z$ 的分布进行训练.
具体而言, 就是在 AE 的损失函数基础上加一个 KL 散度, 用来把 $\mathbf z$ 推向我们预设的分布. 假设我们想让 $\mathbf z$ 满足一个整体分布 $\mathcal N(0, I)$, 那么对应的损失函数就是: $$ \mathcal L = \mathcal L_\text{rec} - D_{KL}(\mathcal N(\boldsymbol{\mu}_{\mathbf z | \mathbf x}, \boldsymbol{\sigma}^2_{\mathbf z | \mathbf x}) || \mathcal N(0, I)) $$ 其中 $\mathcal L_\text{rec}$ 为重建损失.
做个不恰当的比喻:
- VAE 的 $\mathbf z$ 的分布应该像一个球形的云朵, 也就是 $\mathcal N(0, I)$.
- 云朵中有很多球形的小云团, 也就是 $\mathcal N(\boldsymbol{\mu}_{\mathbf z | \mathbf x}, \boldsymbol{\sigma}^2_{\mathbf z | \mathbf x})$
这样我们训练好编码器与解码器以后, 从 $\mathcal N(0, I)$ 中随机采样 $\mathbf z$ 喂给解码器就可以生成图像了.

值得一提的是训练的时候如何对采样这一步进行反向传播. 我们可以将采样描述为: $$\mathbf z = \boldsymbol{\mu}_{\mathbf z | \mathbf x} + \boldsymbol{\sigma}_{\mathbf z | \mathbf x} \cdot \varepsilon$$ 而 $\varepsilon$ 满足 $\mathcal N(0, 1)$ 分布. 这样变成一个等式之后就可以进行反向传播.
VQ-VAE #
其实严格来说 VQ-VAE 与 VAE 没有关系. 唯一的共同点就是: 它们都是类似 AE 的编码器-解码器结构.
具体来说, VQ-VAE 的编码过程如下:
假设原始输入是 $I^{H\times W}$. 那么编码器的输出则是 $\mathbf z^{D\times H^\prime \times W^\prime}$. 其中:
- $D$ 为特征维度
- $H^\prime$ 与 $W^\prime$ 是降采样后的大小.
可以将 $\mathbf z^{D\times H^\prime \times W^\prime}$ 看作是每个像素点上有一个 $D$ 维度的向量. VQ-VAE 维护了一个 Codebook. 其中包含 $K$ 个 $D$ 维度的向量. VQ-VAE 所做的核心步骤就是对每个像素点上的向量 $z_e$ 进行如下的操作:
- 找出 Codebook 中最接近 $z_e$ 的那个向量 $z_q$.
- 用 $z_q$ 替换掉 $z_e$.
这也是为什么会叫 VQ-VAE. VQ 是指 Vector Quantized. 也就是这一步进行的操作.
后面的就是正常的重建了.
为什么 VQ-VAE 效果会变好?
在普通 VAE 中, 我们人为的将 $\mathbf z$ 约束为符合一个连续的高斯分布. 但这就导致模型对于同一类图片的重建结果会平均不同的模式, 导致解码效果模糊.
VQ-VAE 用的是一个离散的 Codebook. 通过 Codebook 中的 code 组合还原输入. 因此输出图像会更清晰.
其实某种意义上可以将 Codebook 看成是一种词嵌入矩阵. 每个像素点相当于一个 Token.
对于 VQ-VAE 的损失可以如下计算: $$ \mathcal L = \mathcal L_\text{rec} + || \text{sg}(\mathbf z_e) - \mathbf z_q ||_2^2 + \beta || \mathbf z_e - \text{sg}(\mathbf z_q) ||_2^2 $$ 其中 $\text{sg}$ 是 stop-gradient 的意思. 意思是阻断梯度. 带有 $\text{sg}$ 项的当作常量对待, 不参与梯度计算. 因此, 中间的一项就是用来更新 Codebook 的. 而最后一项则是用来更新编码器的.
值得一提的是, 由于量化操作是没办法计算梯度的. 因此我们索性就不计算了, 直接透传. 也就是把梯度当成单位矩阵: $$ \frac{\partial \mathbf z_q}{\partial \mathbf z_e} = I $$
最后就是怎么用 VQ-VAE 来生成图像. 到这里可能会发现我们兜兜转转又回到最开始的问题了: 我们不知道 $\mathbf z$ 的分布.
但 VQ-VAE 对 $\mathbf z$ 做了约束: 每个位置上的向量一定是来自 Codebook. 那我只需要对于每个位置从 Codebook 里面选向量填进来, 最后得到的就是一个 $\mathbf z$. 原论文用的生成方法是 PixelCNN. 通过 PixelCNN 预测每个位置上选 Codebook 中的第几个向量. 从而构建出一个 $\mathbf z$, 送到解码器进行重建即可.