模式识别笔记 - 线性分类器 #
什么是线性分类器 #
机器学习中的监督学习任务可以分为两类:
- 回归任务: 旨在寻找输入变量与输出变量的函数关系, 比如预测房价等. 它的输出是连续的.
- 分类任务: 旨在将输入分配到一个定义好的类别中. 它的输出是离散的.
对于分类任务, 一种常用的解决方案是线性分类器. 与贝叶斯分类器相比, 线性分类器是次优的.
贝叶斯分类器在理论上是最佳分类器. 但是它需要知道所有类别的条件概率密度函数才能计算. 由于实际应用中我们无法获得这些概率密度函数, 因此采用线性分类器.
Fisher 线性判别分析 (FLDA) #
FLDA 的思路是监督式降维. 通过找一个最佳的投影方向, 将数据投影上去进行分类. 一个可视化的例子如下:
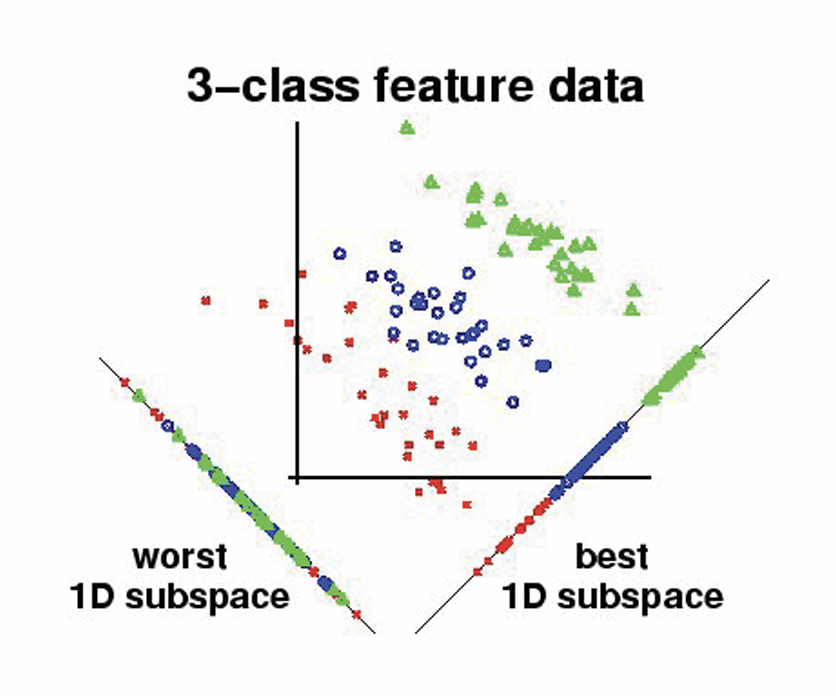
什么样的投影方向是好的呢? 拿上面那幅图来说, 我们希望让同一颜色的投影后尽量聚在一起, 不同颜色的尽量分开. 也就是说:
- 不同类别的数据点尽量远离 (最大化类间方差)
- 同一类别的数据点尽量靠近 (最小化类内方差)
二分类 FLDA #
我们先看如何衡量数据的类内方差. 假设数据有 $M$ 类. 用 $X_i$ 代表第 $i$ 类数据的集合, 其数量为 $N_i$. 那么可以定义第 $i$ 类数据的均值 $\boldsymbol \mu_i$: $$\boldsymbol \mu_i = \frac{1}{N_i}\sum_{\boldsymbol x \in X_i} \boldsymbol x$$ 定义第 $i$ 类数据的散度矩阵 $\boldsymbol S_i$ 为: $$ \boldsymbol S_i = \sum_{\boldsymbol x \in X_i} (\boldsymbol x - \boldsymbol \mu_i) (\boldsymbol x - \boldsymbol\mu_i)^\top $$ 定义数据的类内散度矩阵 $\boldsymbol S_w$ 如下: $$\boldsymbol S_w = \sum_{i=1}^M \boldsymbol S_i$$
类内散度矩阵反映了类内样本相对类均值的偏差
那么投影后的类内散度就可以用 $\boldsymbol{w}^\top S_w \boldsymbol{w}$ 来衡量.
接着来看如何衡量数据的类间方差. 我们先定义数据的整体均值 $\boldsymbol{\mu}$: $$ \boldsymbol{\mu} = \frac{1}{N} \sum_{\boldsymbol{x} \in X} \boldsymbol{x} $$ 之后定义类间散度矩阵 $\boldsymbol{S}_b$ 为: $$ \boldsymbol{S}_b = \sum_{i=1}^M N_i (\boldsymbol{\mu}_i - \boldsymbol{\mu})(\boldsymbol{\mu}_i - \boldsymbol{\mu})^\top $$
类间散度矩阵描述了类中心相对总体中心的偏移方向与强度
那么投影后的类间散度就可以用 $\boldsymbol{w}^\top S_b \boldsymbol{w}$ 来衡量.
由上我们定义 Fisher 判别比 $J_F(\boldsymbol{w})$ 为: $$ J_F(\boldsymbol{w}) = \frac{\boldsymbol{w}^\top \boldsymbol S_b \boldsymbol{w}}{\boldsymbol{w}^\top \boldsymbol S_w \boldsymbol{w}} $$ 最佳的参数 $\boldsymbol{w}^\ast$ 就是使得这个判别比最大的 $\boldsymbol{w}$: $$ \boldsymbol{w}^\ast = \argmax_{\boldsymbol{w}} J_F(\boldsymbol{w}) $$
接下来就是如何求解这个 $\boldsymbol{w}$. 我们通过将分母设为常数, 最大化分子来将其转为一个约束优化问题: $$ \argmax_{\boldsymbol{w}} \boldsymbol{w}^\top \boldsymbol{S}_b \boldsymbol{w} ~~~~\text{s.t.}~~ \boldsymbol{w}^\top \boldsymbol{S}_w \boldsymbol{w} = c \neq 0 $$ 这样就可以用拉格朗日乘子法求解: $$ L(\boldsymbol{w}, \lambda) = \boldsymbol{w}^\top \boldsymbol{S}_b \boldsymbol{w} - \lambda (\boldsymbol{w}^\top \boldsymbol{S}_w \boldsymbol{w} - c) $$ 求梯度有 $$ \frac{\partial L(\boldsymbol{w}, \lambda)}{\partial \boldsymbol{w}} = \boldsymbol{S}_b \boldsymbol{w} - \lambda \boldsymbol{S}_w \boldsymbol{w} $$ 最优解 $\boldsymbol{w}^\ast$ 所处的点梯度为 0, 也就是 $$ \boldsymbol{S}_b \boldsymbol{w}^\ast = \lambda \boldsymbol{S}_w \boldsymbol{w}^\ast $$ 也就是 $$ \boldsymbol{S}_w^{-1} \boldsymbol{S}_b \boldsymbol{w}^\ast = \lambda \boldsymbol{w}^\ast $$ 因此, $\boldsymbol{S}_w^{-1} \boldsymbol{S}_b$ 的特征值就是 $\boldsymbol{w}^\ast$
M-分类 FLDA #
在 不损失类间可分信息 的前提下, 对于 $M$ 分类问题, 类比两点成线, 三点成面. $M$ 类各自的均值点最多能决定一个 $M-1$ 维的超平面. 因此最多能降维到 $M-1$ 维.
对应的, 投影参数为一个矩阵 $\boldsymbol{W} \in \mathbb R^{d\times r}$. 其中 $d$ 为输入维度, $r\leq M-1$ 为投影到的维度.
对应的 Fisher 判别比为: $$ J_F(\boldsymbol{W}) = \frac{|\boldsymbol{W}^\top \boldsymbol S_b \boldsymbol{W}|}{|\boldsymbol{W}^\top \boldsymbol S_W \boldsymbol{W}|} $$ 最佳的参数 $\boldsymbol{W}^\ast$ 就是使得这个判别比最大的 $\boldsymbol{W}$: $$ \boldsymbol{W}^\ast = \argmax_{\boldsymbol{W}} J_F(\boldsymbol{W}) $$
这个可以用广义的特征求解方法进行求解. 投影之后可以用 KNN 等方法再进行分类.
可以证明, 在满足以下条件的时候, FLDA 与最优贝叶斯分类器是等价的:
- 样本足够大
- 每一类都依据相同的条件进行区分
- 样本具有高斯分布且类协方差矩阵相等
感知机 (Perceptron) #
感知机的思路是用优化方法设计最优线性分类器. 也就是定义一个适当的代价函数, 寻求一个算法策略来优化这个代价函数.
它的核心假设是: 可以通过一个线性函数 $g$ 来描述类别之间的决策边界. 即对于一个输入向量 $\boldsymbol{x}$, 计算 $g(\boldsymbol{x})$ : $$ g(\boldsymbol x) = \boldsymbol w^\top \boldsymbol x + b $$ 其中 $\boldsymbol w$ 为与 $\boldsymbol x$ 维度一致的向量. 我们称 $\boldsymbol w$ 为权重向量. 而 $\boldsymbol{x}$ 称为特征向量.
这里我们统一使用列向量.
为了方便起见, 我们记 $\tilde\boldsymbol{x} = \begin{bmatrix} \boldsymbol{x}\\ 1 \end{bmatrix}$, $\tilde{\boldsymbol{w}} = \begin{bmatrix} \boldsymbol{w}\\ b \end{bmatrix}$, 那么原来的公式就可以写成: $$ g(\boldsymbol{x}) = \tilde{\boldsymbol{w}}^\top \tilde{\boldsymbol{x}} $$ 我们称 $\tilde{\boldsymbol{w}}$ 为扩展权重向量, $\tilde{\boldsymbol{x}}$ 为扩展特征向量.
假设我们随便选两个位于判别面上的数据 $\boldsymbol x_1$ 与 $\boldsymbol x_2$, 那么有: $$ g(\boldsymbol x_1) - g(\boldsymbol x_2) = (\boldsymbol w^\top \boldsymbol x_1 + b) - (\boldsymbol w^\top \boldsymbol x_2 + b) = \boldsymbol w^\top (\boldsymbol x_1 - \boldsymbol x_2) = 0 $$ 可见 $\boldsymbol w$ 与 $\boldsymbol x_1 - \boldsymbol x_2$ 是正交的. 也就是说, $\boldsymbol w$ 是判别面的法向量.
二分类感知机 #
我们先讨论一个最简单的场景: 二分类任务, 我们可以将 $g(\boldsymbol x) < 0$ 的分为第一类, 将 $g(\boldsymbol x) > 0$ 的分为第二类. 对应的, $g(\boldsymbol x) = 0$ 就被称作是判别面.
假设类别标签为 $Y=\{+1, -1\}$, 那么分类准则可以写成 $$ \hat y = \text{sign}(g(\boldsymbol{x})) = \begin{cases} +1, & \text{if}~~ \boldsymbol{w}^\top \boldsymbol{x} + b > 0,\\ -1, & \text{if}~~ \boldsymbol{w}^\top \boldsymbol{x} + b < 0, \end{cases} $$
如果用 $y$ 来代表 $\boldsymbol{x}$ 的正确类别, 那么正确分类等价于 $$ y(\boldsymbol{w}^\top \boldsymbol{x} + b) > 0 $$
接下来就是设计代价函数 $J$, 假设一共有 $N$ 个被错误分类的点: $$ J = -\sum_{i=0}^N y_i (\boldsymbol{w}^\top \boldsymbol{x}_i + b) $$
对其求梯度有 $$ \frac{\partial J}{\partial \boldsymbol{w}} = -\sum_{i=0}^N y_i \boldsymbol{x}_i,~~\frac{\partial J}{\partial \boldsymbol{w}} = -\sum_{i=0}^N y_i $$
进行梯度更新有: $$ \boldsymbol{w} \leftarrow \boldsymbol{w} - \alpha \frac{\partial J}{\partial \boldsymbol{w}},~~ b \leftarrow b - \alpha \frac{\partial J}{\partial b} $$ 假设样本线形可分, 那么一定能够在有限的步数后将 $J$ 降到 0.
M-分类感知机 #
对于 $M$-分类感知机, 一个常见的推广是 Kesler’s Construction. 它的思路是, 通过构造 $M$ 个 $\boldsymbol{w}$ 与 $b$ 来进行分类, 取最大的 $g_i(\boldsymbol{x})$ 对应的类别作为预测结果: $$ \hat y= \argmax_{i} g_i(\boldsymbol{x}) = \argmax_{i} \boldsymbol{w}_i \boldsymbol{x}+b_i $$
因此, 对于 $\boldsymbol{x}$, 假设其正确分类为 $y$, 那我们的优化目标就是 $\forall i \neq y$ 都有 $g_y(\boldsymbol{x}) > g_i(\boldsymbol{x})$.
训练时, 我们对于每个样本 $\boldsymbol{x}$ 计算它相对于其他分类的损失.
- 假设样本 $\boldsymbol{x}$ 的正确分类为 $y$
- 那么我们对于所有的 $1 \leq i \leq M$ ($i\neq y$) 计算: $$J = g_y(\boldsymbol{x}) - g_i(\boldsymbol{x}) = (\boldsymbol{w}_y^\top \boldsymbol{x} + b_y) - (\boldsymbol{w}_i^\top \boldsymbol{x} + b_i)$$
- 对其涉及到的 $\boldsymbol{w}_y$, $b_y$, $\boldsymbol{w}_i$ 与 $b_i$ 分别求梯度: $$ \frac{\partial J}{\partial \boldsymbol{w}_y} = \boldsymbol{x},~~~ \frac{\partial J}{\partial {b}_y} = 1,~~~ \frac{\partial J}{\partial \boldsymbol{w}_i} = -\boldsymbol{x},~~~ \frac{\partial J}{\partial {b}_i} = -1 $$
- 对这四个参数进行梯度更新: $$ \begin{aligned} & \boldsymbol{w}_y \leftarrow \boldsymbol{w}_y - \alpha \frac{\partial J}{\partial \boldsymbol{w}_y} && b_y \leftarrow b_y - \alpha \frac{\partial J}{\partial b_y}\\ & \boldsymbol{w}_i \leftarrow \boldsymbol{w}_i - \alpha \frac{\partial J}{\partial \boldsymbol{w}_i} && b_i \leftarrow b_i - \alpha \frac{\partial J}{\partial b_i} \end{aligned} $$
Logistic 回归 (Logistic Regression) #
Logistic 回归不再直接输出类别, 而是输出属于某一类别的概率.
虽然 Logistic 回归名字中带有「回归」二字, 但它并不是用于解决回归问题. 而是用于解决分类问题.
二分类 Logistic 回归 #
Logistic 回归同样是基于线性模型: $$ z = \boldsymbol{w}^\top \boldsymbol{x} + b $$ 但是后面又接了一个 Logistic 函数 (也叫 Sigmoid 函数): $$ \sigma(z) = \frac{1}{1 + e^{-z}} $$ 可见 $0 < \sigma(z) < 1$. 因此我们定义预测的分类 $\hat y$: $$ \hat y = \begin{cases} 1, &\text{if}~~ \sigma(z) \geq 0.5\\ 0, &\text{if}~~ \sigma(z) < 0.5 \end{cases} $$
我们用最大似然估计推导其损失函数. 假设有 $N$ 个样本, 其似然函数为: $$ L(\boldsymbol{w}, b) = \prod_{i=1}^N P(y_i | \boldsymbol{x}_i, \boldsymbol{w}, b) $$ 其中有: $$ P(y_i | \boldsymbol x_i, \boldsymbol{w}, b) = \sigma(\boldsymbol{w^\top x}_i + b_i)^{y_i} (1 - \sigma(\boldsymbol{w^\top x}_i + b_i))^{1-y_i} $$
最大化似然函数就是最小化其负对数形式. 有: $$ -\log L(\boldsymbol{w}, b) = - \sum_{i=1}^N (y_i\log \sigma(\boldsymbol{w^\top x}_i + b_i) +(1-y_i)\log (1 - \sigma(\boldsymbol{w^\top x}_i + b_i))) $$ 求一下均值就得到了其损失函数 $J$:
$$ J = - \frac{1}{N}\sum_{i=1}^N (y_i\log \sigma(\boldsymbol{w^\top x}_i + b_i) +(1-y_i)\log (1 - \sigma(\boldsymbol{w^\top x}_i + b_i))) $$
对其求导可得: $$ \frac{\partial J}{\partial \boldsymbol{w}} = - \frac{1}{N}\sum_{i=1}^N (y_i - \sigma(\boldsymbol{w^\top x}_i)) \boldsymbol{x}_i\\ \frac{\partial J}{\partial b} = - \frac{1}{N}\sum_{i=1}^N (y_i - \sigma(\boldsymbol{w^\top x}_i)) $$
之后进行梯度下降即可.
M-分类 Logistic 回归 #
$M$-分类 Logistic 回归则不再用 Sigmoid. 而是用 Softmax.
类似于 $M$-分类感知机, $M$-分类 Logistic 回归会构造 $M$ 个 $\boldsymbol{w}$.
对于 $\boldsymbol{x}$, 预测其为 $k$ 类别的概率为: $$ P(y=k|\boldsymbol{x}) = \frac{\exp (\boldsymbol{w}_k^\top \boldsymbol{x} + b)}{\sum_{i=1}^M \exp (\boldsymbol{w}_i^\top \boldsymbol{x}+b)} $$
后面的推导大同小异.
支持向量机 (SVM) #
二分类 Hard-Margin SVM #
SVM 的思路很简单, 我们先从简单的线性可分二分类问题着手. 假设有两类样本如图所示, 我们可以设计多个线性分类器. 哪个线性分类器是最好的呢? 很显然应该是具有最大间距的分类器最好.

基于这个想法, 我们尝试最大化间隔从而找到最优的分类器. 我们假设这两条边线为 $$ \begin{cases} \boldsymbol{w}^\top \boldsymbol{x} + b = 1\\ \boldsymbol{w}^\top \boldsymbol{x} + b = -1 \end{cases} $$ 如图所示

我们计算一下这两条边线的垂直距离: 假设 $\boldsymbol{x}_1$ 与 $\boldsymbol{x}_2$ 分别落在两条边线上, 也就是 $$ \begin{cases} \boldsymbol{w}^\top \boldsymbol{x}_1 + b = 1\\ \boldsymbol{w}^\top \boldsymbol{x}_2 + b = -1 \end{cases} $$
我们知道 $\boldsymbol{w}$ 是判别面的法向量, 假设 $\boldsymbol{x}_1$ 投影到 $\boldsymbol{w}$ 上面到长度是 $d_1$, 那么有 $$\boldsymbol{w}^\top\boldsymbol{x}_1 = |\boldsymbol{w}|d_1$$ 同理, 对于 $\boldsymbol{x}_2$ 有 $$\boldsymbol{w}^\top\boldsymbol{x}_2 = |\boldsymbol{w}|d_2$$
而 $d_1 - d_2$ 就是我们要的间隔. 连立四个式子求解可得 $$d_1 - d_2 = \frac{2}{|\boldsymbol{w}|}$$
这样问题就变成了最大化间隔 $\frac{2}{|\boldsymbol{w}|}$. 也就是 $$ \boldsymbol{w}^\ast = \argmax_\boldsymbol{w} \frac{2}{|\boldsymbol{w}|},~~\text{where}~\forall \boldsymbol{x}_i \in X, y_i(\boldsymbol{w}\boldsymbol{x}_i + b) \geq 1 $$ 直接求解不好求, 将其转化为 $$ \boldsymbol{w}^\ast = \argmin_\boldsymbol{w} \frac{|\boldsymbol{w}|^2}{2} = \argmin_\boldsymbol{w} \frac{\boldsymbol{w}^\top \boldsymbol{w}}{2},~~\text{where}~\forall \boldsymbol{x}_i \in X, y_i(\boldsymbol{w}\boldsymbol{x}_i + b) \geq 1 $$
求解的方法是构建拉格朗日函数: $$ \min_{\boldsymbol{w}, b}\max_{\{\lambda\}} L(\boldsymbol{w}, b, \{\lambda\}) = \frac{1}{2}\boldsymbol{w}^\top \boldsymbol{w} + \sum_{i=1}^N \lambda_i (1 - y_i(\boldsymbol{w}^\top\boldsymbol{x}_i + b)) $$
转换为对偶解: $$ \max_{\{\lambda\}}\min_{\boldsymbol{w}, b} L(\boldsymbol{w}, b, \{\lambda\}) = \frac{1}{2}\boldsymbol{w}^\top \boldsymbol{w} + \sum_{i=1}^N \lambda_i (1 - y_i(\boldsymbol{w}^\top\boldsymbol{x}_i + b)) \tag{1} $$
固定 $\{\lambda\}$ 对 $\boldsymbol{w}$ 与 $b$ 求偏导有: $$ \begin{aligned} \frac{\partial L(\boldsymbol{w}, b, \{\lambda\})}{\partial\boldsymbol{w}} &= \boldsymbol{w} - \sum_{i=1}^N \lambda_i y_i \boldsymbol{x}_i\\ \frac{\partial L(\boldsymbol{w}, b, \{\lambda\})}{\partial b} &= \sum_{i=1}^N \lambda_i y_i \end{aligned} $$ 令其都等于零, 得到两个等式: $$ \begin{aligned} \boldsymbol{w}^\ast &= \sum_{i=1}^N \lambda_i y_i \boldsymbol{x}_i\\ \sum_{i=1}^N \lambda_i y_i &= 0 \end{aligned} $$ 代入公式 $(1)$ 可得: $$ \max_{\{\lambda\}} L(\{\lambda\}) = \sum_{i=1}^N\lambda_i - \frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\lambda_i\lambda_j y_i y_j (\boldsymbol{x}_i^\top \boldsymbol{x}_j) $$ 并且要满足两个约束条件: $$ \begin{cases} \sum_{i=1}^N \lambda_i y_i = 0\\ \forall \lambda_i \in \{\lambda\} , \lambda_i \geq 0 \end{cases} $$ 求解出最优的一组 $\{\lambda\}$ 之后求解对应的 $\boldsymbol{w}$ 与 $b$ 即可.
注意到 $\lambda_i$ 与 $\boldsymbol{x}_i$ 是一一对应的. 如果 $\lambda_i \neq 0$, 说明对应的 $\boldsymbol{x}_i$ 落在边界上, 因此这个 $\boldsymbol{x}_i$ 也被称作是支持向量.
二分类 Soft-Margin SVM #
很多时候数据是不满足线性可分的. 只能做到非线性可分.
我们考虑一种情况, 数据本质是线性可分的, 但是由于噪声导致了一些野值点, 造成了训练数据线性不可分. 如图
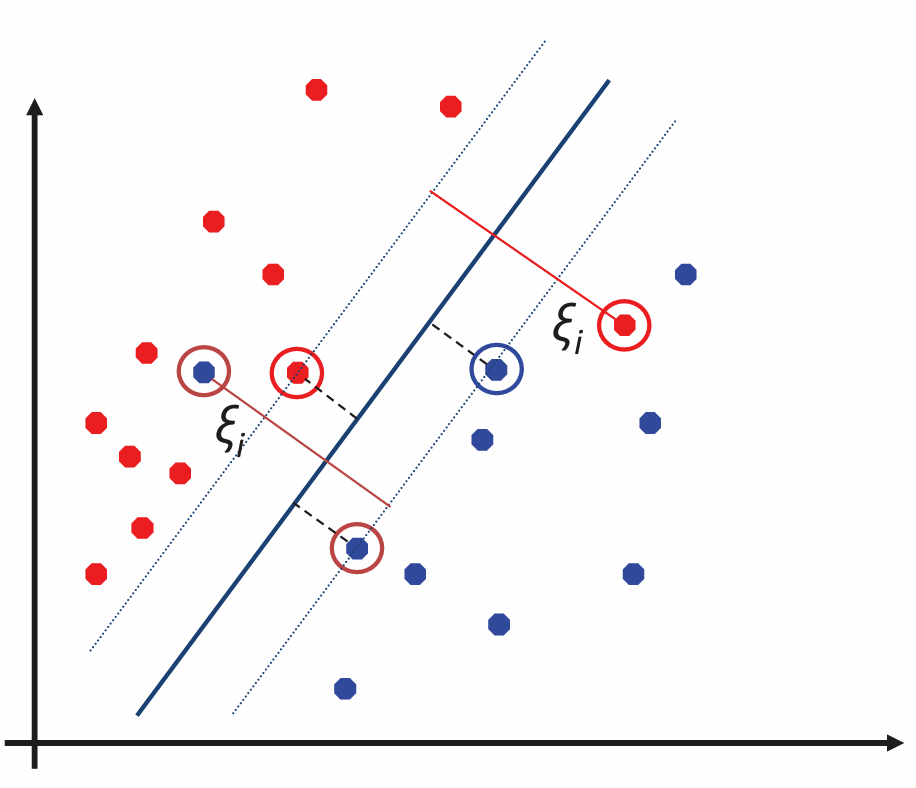
这个时候我们引入一个松弛变量 $\xi_i$ 让其变得线性可分: $$ \begin{cases} \boldsymbol{w}^\top \boldsymbol{x}_i + b \geq + 1 - \xi_i,~\text{for}~y_i = +1\\ \boldsymbol{w}^\top \boldsymbol{x}_i + b \leq -1 + \xi_i,~\text{for}~y_i = -1 \end{cases} $$ 其中 $\xi_i \geq 0$
对应的优化问题就变成了 $$ \boldsymbol{w}^\ast = \argmin_\boldsymbol{w} \frac{\boldsymbol{w}^\top \boldsymbol{w}}{2}+ C\sum_{i=1}^N \xi_i,~~\text{where}~\forall \boldsymbol{x}_i \in X, y_i(\boldsymbol{w}\boldsymbol{x}_i + b) \geq 1 - \xi_i, $$ 其中的 $C$ 决定着噪声的容忍度. $C$ 越大, 越不允许出现错误分类点.
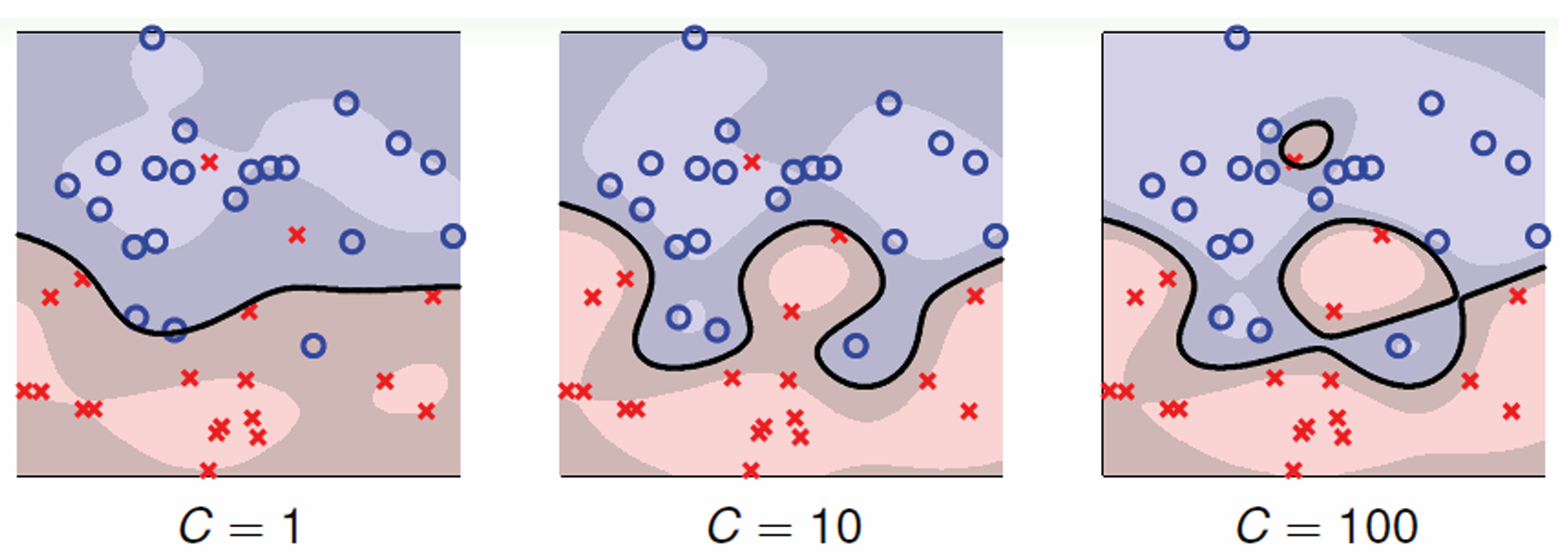
剩下的方法大同小异.
多分类 SVM #
多分类 SVM 是二分类 SVM 的扩展版本. 常见的多分类 SVM 有几种:
- 一对多 SVM: 训练 $M$ 个分类器, 每个分类器负责区分是否为第 $i$ 类.
- 一对一 SVM: 训练 $M(M-1)/2$ 个分类器, 每个分类器负责区分是两类中的哪一类.
- 直接优化多分类 SVM (Crammer-Singer 方法): 类似 $M$-分类感知机的 Kesler’s Construction.
由于篇幅原因就不再展开. 有兴趣的读者可以自行查阅.
附录: 分类任务常用指标 #
对于二分类任务, 可以得出如下混淆矩阵:
| 预测为正类 | 预测为负类 | |
|---|---|---|
| 实际为正类 | TP (真阳性) | FN (假阴性) |
| 实际为负类 | FP (假阳性) | TN (真阴性) |
可以有如下指标:
- 准确率 (Accuracy), 用于衡量所有预测中预测正确的比例
- 缺点是类别不平衡时会严重误导 $$ \text{Accuracy} = \frac{TP + TN}{TP+TN+FP+FN} $$
- 精确率 (Precision), 用于衡量预测为正的样本中, 真正是正的比例
- 关注的是预测为正类的可靠性 $$ \text{Precision} = \frac{TP}{TP+FP} $$
- 召回率 (Recall), 用于衡量正样本中被预测为正的比例
- 关注的是没漏掉的程度 $$ \text{Recall} = \frac{TP}{TP+FN} $$
- F1-score, 用于平衡 Precision 与 Recall, 为其调和平均数 $$ \text{F1}=2\times \frac{\text{Precision} \times \text{Recall}}{\text{Precision} + \text{Recall}} $$
可以通过求平均的方式推广到多分类任务上:
- Macro 平均:对每个类别单独算指标再取平均, 例如 Macro-Precision 的计算公式为: ($C$ 为类别数) $$ \text{Macro-Precision}=\frac{1}{C}\sum_{i=1}^C \text{Precision}_i $$
- Micro 平均:所有类别样本混合后再整体计算, 例如 Micro-Precision 的计算公式为: ($C$ 为类别数) $$ \text{Micro-Precision}=\frac{\sum_i TP_i}{\sum_i(TP_i+FP_i)} $$
- Weighted 平均:根据类别样本数量加权平均
适用场景如下:
| 指标 | 适用场景 |
|---|---|
| Macro 平均 | 想看每个类别是否都表现良好,关心小类性能 |
| Weighted 平均 | 想要一个总体性能指标,同时又考虑类别比例 |
| Micro 平均 | 直接关心总体样本级表现(准确率式评估) |
除此以外还可以绘制 ROC (Receiver Operating Characteristic) 曲线. 用于衡量分类器在不同分类阈值下的性能. 如图, ROC 曲线下方的面积被称为是 AUC (Area Under Curve), 越大越好.
